CURSO FÍSICA: EJERCICIOS DE ANÁLISIS VECTORIAL.

» Asesor Académico: Andersson De La Cruz Arbildo

Ejercicios:

1. La resultante entre dos vectores de 10 y 15 unidades es 20 unidades. Calcular el ángulo que forman las componentes.

Solución:

Por la ley de cosenos: \begin{equation} \begin{aligned} R^2 & = A^2 + B^2 + 2AB cos \theta \\ 20^2 & = 10^2 + 15^2 + 2.10.15 cos \theta \\ cos \theta & = \frac{1}{4} \\ \theta & = arcCos (\frac{1}{4}) \\ \theta & \approx 75.52° \end{aligned} \end{equation}

2. A partir de los vectores mostrados, calcule un vector perpendicular al plano determinado por los vectores \( \vec{A} \) y \( \vec{B} \), el cual tiene un módulo de \( \sqrt{13} \).

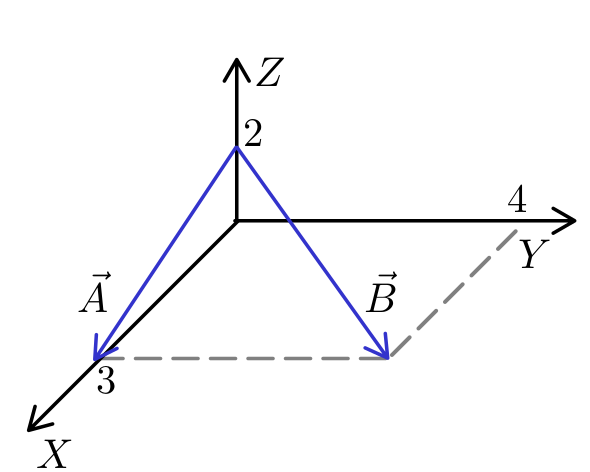
Solución:

Reescribimos los puntos dados en coordenadas rectangulares.

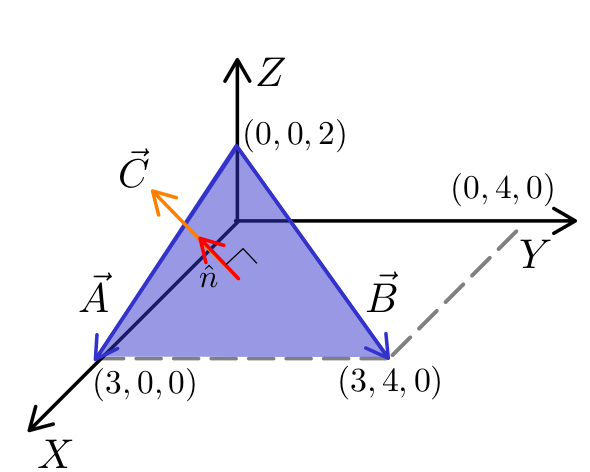
Calculamos \( \vec{A} \) y \( \vec{B} \) : \begin{equation} \begin{aligned} \vec{A} & = (3,0,0) - (0,0,2) = (3,0,-2) \\ \vec{A} & = 3 \hat{i} + 0 \hat{j} - 2 \hat{k} \\ \vec{B} & = (3,4,0) - (0,0,2) = (3,4,-2) \\ \vec{B} & = 3 \hat{i} + 4 \hat{j} - 2 \hat{k} \end{aligned} \end{equation} Aplicamos el producto vectorial para hallar un vector \( \vec{N} \) perpendicular al plano \begin{equation} \vec{N}=\vec{A} \text{x} \vec{B}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 0 & -2 \\ 3 & 4 & -2 \end{vmatrix} = 8\hat{i} + 0 \hat{j} + 12 \hat{k} \end{equation} , luego hay que calcular el vector unitario perpendicular al plano. \begin{equation} \hat{n}=\frac{\vec{N}}{N} \end{equation} \begin{equation} N = \sqrt{ 8^2 + 0^2 +12^2 } = \sqrt{208} \end{equation} Me piden hallar el vector \( \vec{C} \) que es paralelo a \( \hat{n} \) y tiene módulo \( \sqrt{13} \), entonces \begin{equation} \begin{aligned} \vec{C} & = \sqrt{13} \hat{n} \\ \vec{C} & = \sqrt{13} \frac{8\hat{i} + 0 \hat{j} + 12 \hat{k}} {\sqrt{208}} \\ \vec{C} & = \frac{8\hat{i} + 0 \hat{j} + 12 \hat{k}} {\sqrt{16}} \\ \vec{C} & = \frac{8\hat{i} + 0 \hat{j} + 12 \hat{k}} {4} \end{aligned} \end{equation} $$ \boxed{\vec{C} = 2\hat{i} + 0 \hat{j} + 3 \hat{k}} $$

3. Dos vectores \( \vec{a} \) y \( \vec{b} \) forman un ángulo de 120°. Si \( a=3 \) y \( b=4 \); calcule el producto escalar \( (3\vec{a}-2\vec{b}).(\vec{a}+2\vec{b}) \)

Solución:

Recordar el producto escalar de 2 vectores es : $$ \vec{P}.\vec{Q}=PQ Cos \theta $$ Se desarrolla el producto de la siguiente forma \begin{equation} \begin{aligned} (3\vec{a}-2\vec{b}).(\vec{a}+2\vec{b}) & = 3 \vec{a} . \vec{a} + 3 \vec{a} . 2 \vec{b} - 2 \vec{b}.\vec{a} - 2\vec{b}.2\vec{b} \\ & = 3a^2+4\vec{a}.\vec{b} - 4b^2 \\ & = 3a^2+4abCos(120°) - 4b^2 \\ & = 3.3^2+4.3.4.\frac{-1}{2} - 4.4^2 \end{aligned} \end{equation} $$ \boxed{(3\vec{a}-2\vec{b}).(\vec{a}+2\vec{b})=-61} $$

4. Calcule la resultante de los vectores mostrados, en función de los vectores unitarios \( \hat{u}_1 \) y \( \hat{u}_2 \).

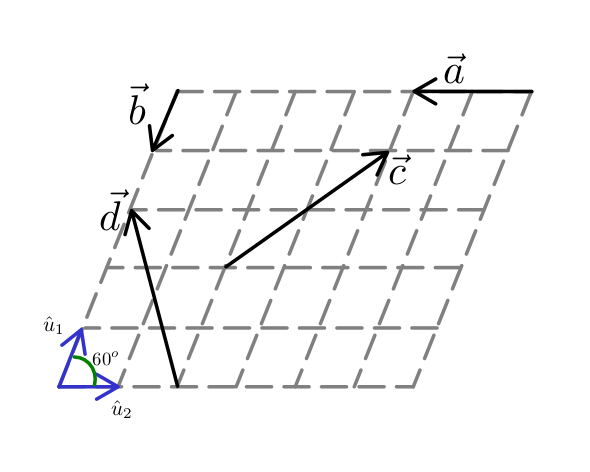
Solución:

Representamos cada vector en función de las bases \( \hat{u}_1 \) y \( \hat{u}_2 \), \begin{equation} \begin{aligned} \vec{a} & = -2 \hat{u}_2 \\ \vec{b} & = - \hat{u}_1 \\ \vec{c} & = 2 \hat{u}_1 + 2 \hat{u}_2 \\ \vec{d} & = 3 \hat{u}_1 - 2 \hat{u}_2 \end{aligned} \end{equation} luego , sumamos los vectores: \begin{equation} \begin{aligned} \vec{R} & = \vec{a} + \vec{b} + \vec{c} + \vec{d}\\ \vec{R} & = (-1+2+3) \hat{u}_1 + (-2+2-2)\hat{u}_2\\ \end{aligned} \end{equation} $$ \boxed{ \vec{R}= 4 \hat{u}_1 -2 \hat{u}_2 } $$

5. A partir del sistema mostrado, calcule el módulo de la resultante.

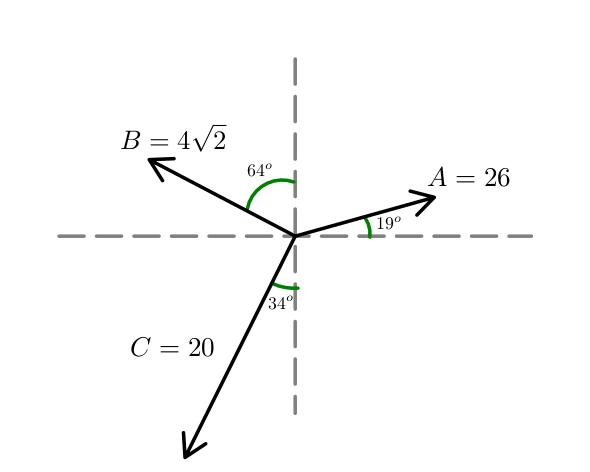
Solución:

Vemos que los vectores forman ángulos poco conocidos con los ejes X e Y, entonces lo que se propone es girar todos los vectores 19° en sentido horario, luego se aprecia que los nuevos ángulos formados con los ejes X e Y son conocidos y procedemos con la descomposición rectangular.

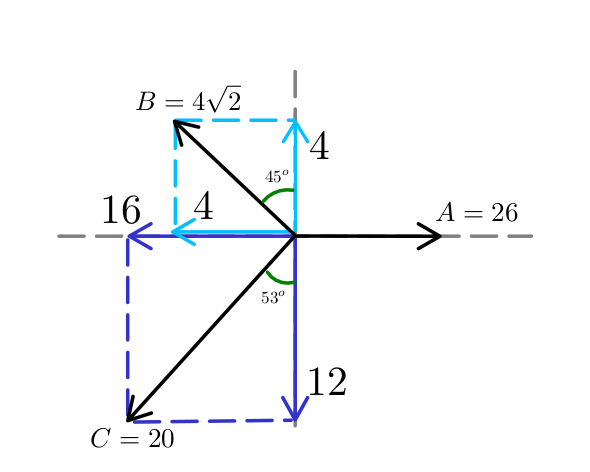
Finalmente escribimos las coordenadas de los vectores rotados, \begin{equation} \begin{aligned} \vec{A} & = (26,0)\\ \vec{B} & = (-4,4)\\ \vec{C} & = (-16,-12) \end{aligned} \end{equation} y procedemos a calcular la resultante. \begin{equation} \begin{aligned} \vec{R} & = \vec{A}+\vec{B}+\vec{C}\\ & = (26,0)+(-4,4)+(-16,-12)\\ & = (6,-8) \end{aligned} \end{equation}

Recuerden que cuando rotamos los vectores solo cambia el ángulo que forma con el eje X e Y pero el módulo no cambia. Entonces el módulo del vector \( \vec{R} \) rotado es el mismo módulo que \( \vec{R} \) sin rotar.

\begin{equation} \begin{aligned} \| \vec{R} \| & = \sqrt{(6)^2 + (-8)^2} \\ & = \sqrt{36 + 64} \end{aligned} \end{equation} $$ \boxed{\| \vec{R} \| = 10} $$

6. Si la arista del cubo es de 2u, determine el módulo de la resultante de los vectores mostrados.

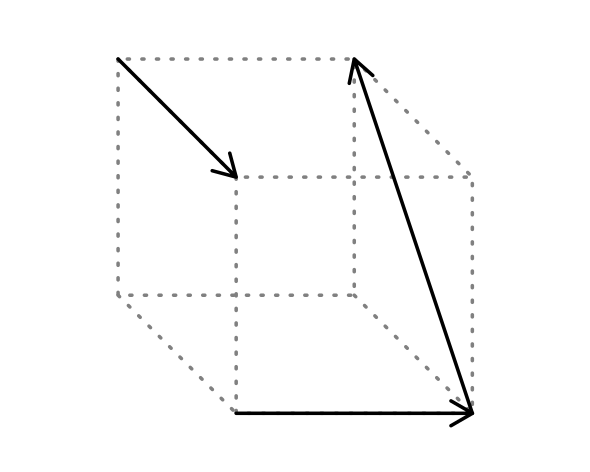
Solución:

Nos damos cuenta que el vector \( \vec{b} \) y \( \vec{c} \) son consecutivos y si transladamos el vector \( \vec{a} \) hacia abajo, entonces así los tres vectores serán consecutivos. En este caso usamos el método del polígono en 3 dimensiones, donde finalmente la resultante seria el vector \( \vec{R} \) indicado en el gráfico.

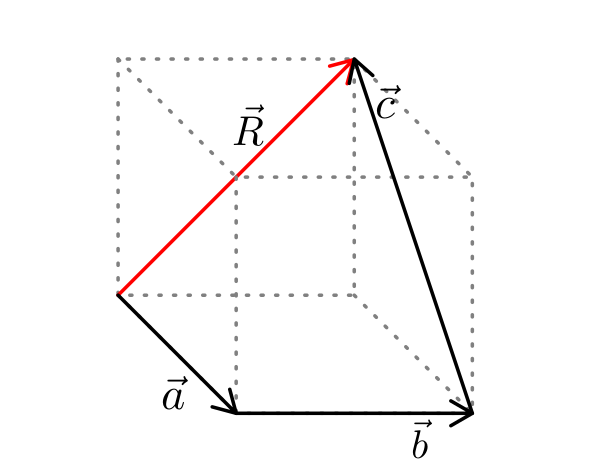
Dado que cada lado mide 2u, usamos el teorema de Pitágoras para calcular el módulo de la resultante \begin{equation} \begin{aligned} \| \vec{R} \| & = \sqrt{2^2 + 2^2} \\ & = \sqrt{8} \end{aligned} \end{equation} $$ \boxed{\| \vec{R} \| = 2\sqrt{2}u} $$

7. Si el vector \( \vec{X} \) se puede expresar de la forma \( \vec{X} = c \vec{A} + d \vec{B} \) , donde c y d son números enteros, determine c + d.

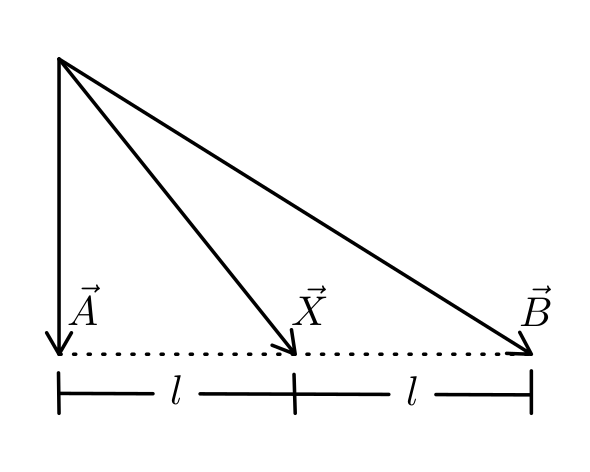
Solución:

El gráfico nos indica que \( \vec{X} \) llega al punto medio de la base del triángulo (en Q), luego trazamos los vectores \( \vec{L} \) en la base, ver el gráfico.

En el triángulo MNQ la suma de vectores es, $$ \vec{X} = \vec{A} + \vec{L} \ ...\ (i)$$ y en el triángulo NQP la suma de vectores es, \begin{equation} \begin{aligned} \vec{B} & = \vec{X} + \vec{L} \\ \vec{X} & = \vec{B} - \vec{L} \ ...\ (ii) \end{aligned} \end{equation} Sumamos las ecuaciones (i) y (ii), \begin{equation} \begin{aligned} \vec{X} + \vec{X} & = \vec{A} + \vec{L} + \vec{B} - \vec{L} \\ 2\vec{X} & = \vec{A} + \vec{B} \\ \vec{X} & = \frac{1}{2}. \vec{A} + \frac{1}{2}. \vec{B} \end{aligned} \end{equation} , entonces se determina que \( c=d=\frac{1}{2} \) y nos piden \( \boxed{ c+d= \frac{1}{2} + \frac{1}{2} = 1} \).

8. En la figura mostrada \( \vec{P} = r\vec{A} + n\vec{B}\). Hallar el valor numérico de "r" y "n". Cada cuadrado es de lado 1cm.

Solución:

Escribimos las coordenadas de los vectores \begin{equation} \begin{aligned} \vec{A} & = (-3,-2) \\ \vec{B} & = (-1,3) \\ \vec{P} & = (2,-3) \end{aligned} \end{equation} y reemplazamos los valores encontrados en la ecuación anteriormente mencionada, \begin{equation} \begin{aligned} \vec{P} & = r\vec{A} + n\vec{B} \\ (2,-3) & = r(-3,-2) + n(-1,3) \\ (2,-3) & = (-3r,-2r) + (-n,3n) \\ (2,-3) & = (-3r-n,-2r+3n) \end{aligned} \end{equation} Igualamos cada término, \begin{equation} \begin{aligned} 2 & =-3r-n \\ (2 & =-3r-n) \text{x} 3 \\ 6 & =-9r-3n \ ...\ (i)\\ \\ -3 & =-2r+3n \ ...\ (ii) \end{aligned} \end{equation} , y sumamos las ecuaciones (i) y (ii). \begin{equation} \begin{aligned} 6-3 & =-9r-3n -2r+3n \\ 3 & = -11 r \end{aligned} \end{equation} $$\boxed{r = -\frac{3}{11}}$$ reemplazando "r" en la ecuación (ii), tenemos $$ -3 =-2 ( -\frac{3}{11} ) +3n $$ $$ \boxed{n = -\frac{13}{11}} $$

9. Se muestra un cuadrado de lado 8u. Determine el módulo de la resultante de los tres vectores mostrados. Considere de A y B son puntos medios de sus respectivos lados.

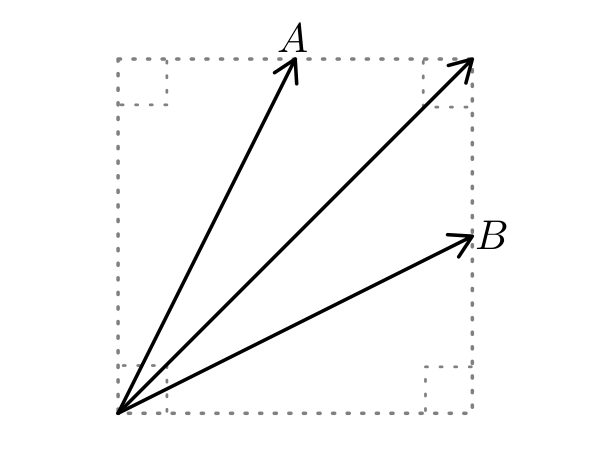
Solución:

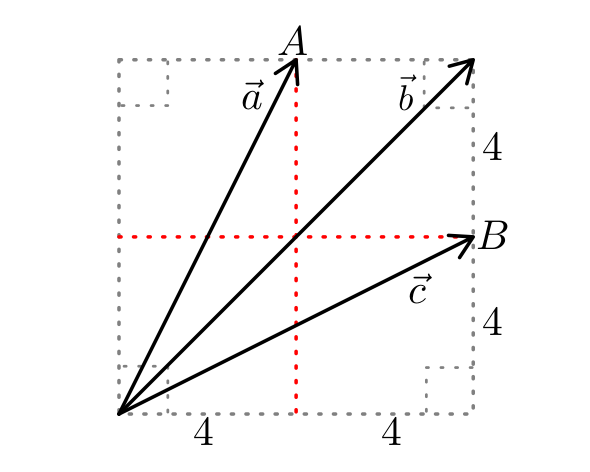
Escribimos las coordenadas de los vectores, \begin{equation} \begin{aligned} \vec{a} & = (4,8) \\ \vec{b} & = (8,8) \\ \vec{c} & = (8,4) \\ \end{aligned} \end{equation} , hallamos el vector resultante. \begin{equation} \begin{aligned} \vec{R} & = \vec{a} + \vec{b} + \vec{c} \\ & = (4,8) + (8,8) + (8,4) \\ & = (20,20) \\ \end{aligned} \end{equation} Entonces el módulo de la resultante es $$ \| \vec{R} \| = \sqrt{20^2 + 20^2} $$ $$ \boxed{\| \vec{R} \| = 20 \sqrt{2}} $$

10. Si el gráfico mostrado es un trapecio, determine el módulo de la resultante de los vectores mostrados, considere que m es punto medio de ab.

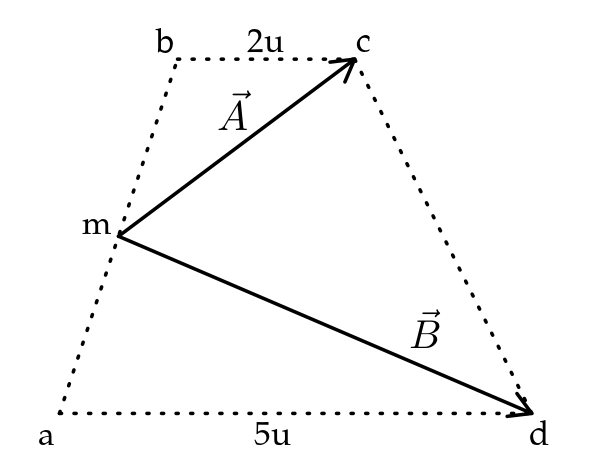
Solución:

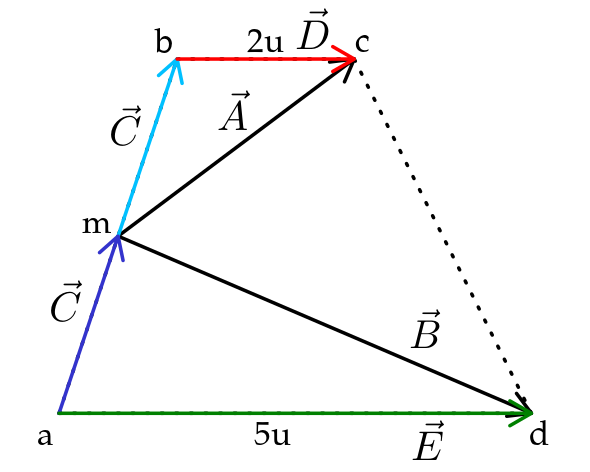
Trazamos los vectores \( \vec{C} \), \( \vec{D} \) y \( \vec{E} \), luego analizamos el triángulo mbc $$ \vec{A} = \vec{C} + \vec{D}\ ...\ (i)$$ y usamos el triángulo amd \begin{equation} \begin{aligned} \vec{E} & = \vec{C} + \vec{B} \\ \vec{B} & = \vec{E} - \vec{C}\ ...\ (ii) \end{aligned} \end{equation}

Finalmente sumamos las ecuaciones (i) y (ii) para hallar la resultante. \begin{equation} \begin{aligned} \vec{R} & = \vec{A} + \vec{B} \\ & = \vec{C} + \vec{D} + \vec{E} - \vec{C}\\ & = \vec{D} + \vec{E} \end{aligned} \end{equation} Como \( \vec{D} \) y \( \vec{E} \) son paralelos y tienen el mismo sentido, el módulo del vector resultante seria la suma de los módulos, de los vectores compomentes.

$$ \| \vec{R} \| = \| \vec{D} \| + \| \vec{E} \| $$ $$ \boxed{\| \vec{R} \| = 2u + 5u = 7u} $$

Contacta con nosotros:

Si usted, tiene alguna consulta acerca de las asesorías de física o matemáticas que brindamos (vía ZOOM); puede contactarnos a nuestro número telefónico 912-580-118 o a través de nuestro Formulario de Contacto.

Más información sobre nosotros:
✍ Oficinas: Av. Alfredo Mendiola 5127 Urb. Parque Naranjal, Los Olivos, Lima, Perú.
✍ Especialista: Andersson David De La Cruz Arbildo.
✍ Sitio web: Curso de Física.
✍ Teléfonos: 912-580-118.